grandparent(X,Y) :- parent(X,Z), parent(Z,Y).
where X, Y and Z are variables, according to the Prolog convention of capitalising variables.
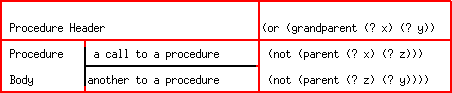
Let us write Horn clauses as, for example:
(or (grandparent (? x) (? y))
(not (parent (? x) (? z)))
(not (parent (? z) (? y))))
2 Viewing Clauses as Procedures
Such a clause can be regarded as a kind of a definition of a procedure grandparent. From this operational viewpoint, (? x) and (? y) are formal parameters of the procedure, while (? z) is a local variable. Whereas in Scheme all parameters are called by value, in the operational interpretation of the logic paradigm we regard all parameters as being called by reference. So if we regard the clause above as a kind of procedure definition we see the following correspondence:
So, the negated form of our theorem, for example
(not (grandparent Liz (? p)))
can be regarded as a call of our procedure grandparent.
2.1 Matching constant parameters
Notice that one difference between this and Pascal is that if you pass a constant as actual parameter, instead of getting an error report if you try to bind it inside the procedure, a logic language will try to match the constant. Here you could think of the (? p) in the call as a kind of call-by-reference (although the logic paradigm extends this concept rather far).
2.2 Procedure Activations Persist after Procedure returns result
Another important difference is that the grandparent procedure activation does not cease to exist when it returns a result. Rather it is kept around to be re-activated if the result is not satisfactory. This corresponds to the fact that a clause can be resolved with several other clauses.
[Some implementations of Scheme allow you to write Scheme functions that have the same property - they provide a function named call/cc (call with current continuation) which preserves the state of a computation to be re-activated at a later time.]
2.3 Procedure Definitions may be Distributed over Clauses
Finally, let us notice that the definition of a predicate-procedure can be spread over more than one case. For example, suppose we had expressed our family relations in terms of mother and father then we might have
(or (grandmother (? x) (? y))
(not (mother (? x) (? z))) (not (mother (? z) (? y))))
(or (grandmother (? x) (? y))
(not (mother (? x) (? z))) (not (father (? z) (? y))))
We shall see this kind of distribution of a definition among several statements that may be widely separated in the program text in the Object Oriented Paradigm.
2.4 Unit Clauses Record Basic Facts
Now let us consider unit clauses. Operationally two clauses such as
(parent Liz Charley)
(parent Charley Will)
can be regarded as defining a single procedure parent. We could think of this as a succinct way of defining a conditional.
So let us consider the query
(not (grandparent Liz (? p)))
this "calls the procedure" grandparent, requiring us to perform the calls
(not (parent Liz (? z))) (not (parent (? z) (? p)))
performing the first call of parent
we bind (? z) to Charley. Performing the
second call, we bind the variable (? p) to the value
Will.
3 Arithmetic and other operations can be built in
Computers have a lot of built-in arithmetic capability. We could construct our arithmetic from logical first principles, for example by translating the Peano postulates into predicate calculus. However it would be much more efficient to make use of built-in arithmetic capabilities.
3.1 Building in arithmetic predicates like <
Consider the "less-than" relationship of arithmetic. A good implementation of the logic paradigm should behave exactly as if there were an infinite number of unit clauses such as
(or (< 1 2))
(or (< 1 3))
(or (< 1 4))
...
(or (< 2 3))
...
It should be noted that the best-known implementation of the Logic Paradigm, namely the Prolog language, has a half-baked implementation of arithmetic comparison - both arguments of < and other arithmetic operators have to be instantiated to numbers if an error message is to be avoided.
3.2 Building in arithmetic functions like +
Arithmetic functions can also be built in. Given that logic programs behave as procedural rather than functional languages, the most consistent way of implementing such functions would be to represent them as predicates. For example one might write (add 2 3 (? x)) and expect (? x) to be bound to 5. However this is a very tedious way of specifying arithmetic, so the convention is to introduce an evaluation predicate which evaluates an expression. In our Scheme-based formalism one would write:
(is (? x) (+ 2 3))
Again, the logic-languages behave to some extent as if there were an infinite number of unit clauses which said, for example
(is 5 (+ 2 3))
however they do not behave consistently.
Exercise:
Would the Peano postulates translate into first-order predicate calculus?4 Function symbols provide the ability to create data-structures.
So far we have confined ourselves in our examples to what is often called the "datalog" paradigm, that is to say the arguments of the predicates have been simple variables, numbers or other constants. At this level, the capabilities of languages of the logic paradigm such as Prolog, and the capabilities of relational databases are very similar. In a sense, logic languages tend to work more lazily - they "think" of a way of satisfying a predicate and postpone thinking of any other way until the first way is proved wrong. Relational databases work more eagerly. In the grandparent case, a relational database would think of all the possible pairs of people who had that relationship and then might allow the user to choose the particular one she wanted.
However our version of the predicate calculus allows us to have function symbols. These allow us in effect to build data-structures.
4.1 Determining if a given element is a member of a list
(or (member (? x) (cons (? x) (? y)))) ;(1)
(or (member (? x) (cons (? y) (? z))) (not (member (? x) (? z)))) ;(2)
Now consider the "goal":
(not (member 2 (cons 1 (cons 2 (cons 3 nil))))) ;(3)
This generates the sub-goal, with the substitution ((? y) . 1)
(not (member 2 (cons 2 (cons 3 nil))))
And now with the substitution ((? x) . 2), we get the empty clause by resolution with (1). So the original goal is satisfied.
Now consider:
(or (not (member (? p) (cons 1 (cons 2 (cons 3 nil)))))
(not (> (? p) 1))) ;(4)
This resolves with (1) to give the binding ((? p) . 1) and the new goal
(not (> 1 1))
However this goal cannot be satisfied by resolution against anything in the (implicit) database of numeric facts since the (false) fact (or (> 1 1)) does not occur in there. So our first result from the member procedure is no good. However we can resuscitate it, by using clause (2)! From (4) and (2) we obtain
(or
(not (member (? x) (cons 2 (cons 3 nil))))
(not (> (? p) 1)))
The first clause now resolves against (1) giving ((? x) . 2) , leaving us with
(not (> 2 1))
which resolves against the implicit clause (or (> 2 1)) in the database, leaving us the empty clause.
4.2 Building a new list with concatenation
Now let us consider a more complicated example. We might define append as:
(or (append nil (? list) (? list))) ;[1]
(or ;[2]
(append
(cons (? x) (? list1))
(? list2)
(cons (? x) (? list3)))
(not
(append (? list1) (? list2) (? list3))))
Now consider the goal:
(not (append (cons 1 nil) (cons 2 nil) (? listout))) ;[3]
This resolves with [2] with the unification
( ;[U1]
((? x) . 1)
((? list1) . nil)
((? list2) (cons 2 nil))
((? listout) (cons 1 (? list3)))
)
giving the new goal
(not (append nil (cons 2 nil) (? list3))) ;[4]
we can now use clause [1] to obtain the unification
(((? list3) (cons 2 nil))) ;[U2]
satisfying the goal, since [1] is a unit clause. We can get the actual value of (? listout) by using the two unifying substitutions [U1] and [U2]. From U1 we obtain
(cons 1 (? list3))
as the value for (? listout), and from [U2] this is seen to be
(cons 1 (cons 2 nil))