2.1 The generic implementation of list->set
2.2 The generic implementation of intersect
2.3 The generic implementation of included_in?
2.4 The generic implementation of equal_set?
Sets as unordered lists 3.1 Implementing the empty set as an unordered list
3.2 Implementing set->list representing sets as unordered lists
3.3 Implementing member_set? representing sets as unordered lists
3.4 Implementing adjoin representing sets as unordered lists
3.5 Use the generic functions for intersect equal_set?
Sets as ordered lists 4.1 Implementing the empty set as an ordered list
4.2 Implementing set->list representing sets as ordered lists
4.3 Implementing member_set? representing sets as ordered lists
4.4 Implementing adjoin representing sets as ordered lists
4.5 We have a big win implementing intersect on ordered lists
Sets as Trees - an Introduction
A set is a fundamental concept of mathematics. Unfortunately, there is no single uniform representation of set that meets all our needs as computer scientists. The most important distinction is between finite and infinite sets. A finite set can be represented by some kind of explicit enumeration in a data-structure, whereas an infinite set must be represented by some kind of description that does not explicitly enumerate the elements. Of course, it is not always practicable to enumerate large finite sets.
We shall study three representations of finite sets from the point of view of a small number of basic operations on sets:
empty_set The representation of the empty set.
(list->set l) Creates a set which consists of the elements of a
list.
(set->list s) Creates a list of the elements of the set in an
undefined order. This will be the identity function
for representations of sets as lists.
(member_set? x s) Computes whether a given object x is a member of a
set s.
(included_in? s1 s2) Computes whether each member of s1 is a member of s2
(equal_set? s1 s2) Computes whether two sets s1 s2 are the same set.
(adjoin x s) Makes a new set by adding the element x to the set s.
(intersect s1 s2) Computes the intersection of the two sets s1, s2.
In particular we need to study the relationship between the representation and how fast we can make these basic operations run - their time complexity.
The 3 representations are
Unordered lists: A set {1,2,3} may be represented as the list (3 1 2)
Ordered lists: A set {1,2,3} will be represented as the list (1 2 3)
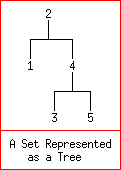
Binary trees: A set {1,2,3,4,5} may be represented as the tree:

All of these representations require that we be able to compare for equality elements which occur in sets. The ordered list and tree representations require that an ordering relation be defined on the elements. For simplicity, we shall confine ourselves to sets of numbers, where <= is an ordering relation.
We can regard the functions set->list, member_set?, adjoin together with empty_set as being basic operations which we have to define for all representations of sets. Using these, we can provide generic implementations of list->set, included_in?, equal_set? and intersect. While these generic implementations will always work, they will not always be the fastest possible implementation for a given representation, since we may be able to exploit the special properties of that representation.
We can convert a list to a set by repeated application of the adjoin operation, giving us the function:
(define (list->set l)
(if (null? l) empty_set
(adjoin (car l) (list->set (cdr l)))
)
)
We can conveniently make use of the reduce function that we defined earlier in the course to save us writing some explicit recursions.
(define (reduce f acc base l)
(if (null? l)
base
(acc (f (car l)) (reduce f acc base (cdr l)))))
Using reduce we can write a generic intersect function. This converts one of the sets to a list, and then uses an accumulator function in which member_set? is used to determine if each member of the list is a member of the other set. If it is, it is combined into the result, and if not it isn't. The base is simply the empty_set.
(define (intersect s1 s2)
(reduce
(lambda (x) x) ;f
(lambda (x s) ;acc
(if (member_set? x s2)
(adjoin x s)
s)
)
empty_set ;base
(set->list s1) ;list
)
)
(define (included_in? s1 s2)
(reduce
(lambda (x) (member_set? x s2)) ;f
andf ;acc
#t ;base
(set->list s1)) ;list
)
(define (andf b1 b2)
(and b1 b2)
)
(define (equal_set? s1 s2)
(and (included_in? s1 s2) (included_in? s2 s1))
)
A set can be represented as a list with no duplicates. The fact that the list contains no duplicates can be regarded as an invariant for this representation.
The empty set is simply implemented as the empty list.
(define empty_set '())
In this representation set->list is the identity function (but note that list->set has to remove duplicates).
(define set->list (lambda (x) x))
To implement set membership, we can use the built-in member function, but ensure that an actual boolean value is returned.
(define (member_set? x s)
(if (member x s) #t #f)
)
This takes O(n) time, since member takes O(n) time to go through the list and compare each element for equality with x.
For (adjoin x s) we need to test membership and only cons on x to the list representing s if it is not already there. This preserves the "no duplicates" invariant.
(define (adjoin x s)
(if (member_set? x s)
s
(cons x s)
)
)
This takes O(n) time, since member_set? takes O(n) time.
We can use the generic definitions of intersect and equal_set?. These both take O(n^2) time.
Provided we have compiled Lecture 12, we can test out our implementation using the testing functions contained in that lecture.
(test_laws_sets 100)
If we add the additional requirement (invariant) that our sets be represented as lists with the elements placed in order, we find that intersection can be done more efficiently.
As before, the empty_set is represented by the empty list.
(define empty_set '())
As before, set->list is simply the identity function.
(define set->list (lambda (x) x))
We can make member_set? rather more efficient. Assuming a uniform distribution of values of x we can halve the expected time for an evaluation of ( member_set x s) in the cases in which x actually is a member of s by using the fact that if the first member of s larger than x we cannot possibly find x in s (see (1) below). However member_set? still remains O(n).
(define (member_set? x s)
(cond
((null? s) #f)
((= x (car s)) #t)
((> (car s) x) #f) ; (1)
(else (member_set? x (cdr s)))
)
)
In this representation, adjoin still takes O(n) time, since we have in the worst case to examine the entire list. For example: (adjoin 5 (list->set '(1 2 3 4))) ==> (1 2 3 4 5)
But we can achieve a small improvement if we recognise that if the first member of the list representing the set is greater than the element we are adjoining, then we don't have to look any further.
(define (adjoin x s)
(cond
( (null? s) (list x))
( (< x (car s)) (cons x s))
((= x (car s)) s)
(else (cons (car s) (adjoin x (cdr s))))
)
)
However we can improve our implementation of intersect significantly by exploiting the fact that the two sets are represented as ordered lists. To do this we employ a kind of algorithm known as merging.
The function below, based on merging, takes O(n) where n is the maximum of the size (cardinality) of the two sets. The idea is that we go through the ordered lists in "lock step" successively comparing the first elements and deciding on the basis of the comparison whether to incorporate them in the result, always taking the cdr of the list with the smaller first element.
'(2 3 4 6 7)
'(1 3 5 6) First element not in the intersection, take cdr
'(2 3 4 6 7) First element not in the intersection, take cdr
'(3 5 6)
'(3 4 6 7) First elements are in the intersection, take cdr
'(3 5 6) of both, incorparate car's in the result.
'(4 6 7) First element not in the intersection, take cdr
'(5 6)
'(6 7)
'(5 6) First element not in the intersection, take cdr
'(6 7) First elements are in the intersection, take cdr
'(6) of both, incorporate car's in the intersection.
'(7)
'() No elements in the intersection.
(define (intersect s1 s2)
(if (or (null? s1) (null? s2)) '()
(let (
(x1 (car s1))
(x2 (car s2))
); end let binding
(cond
((= x1 x2) (cons x1 (intersect (cdr s1) (cdr s2))))
((< x1 x2) (intersect (cdr s1) s2))
(else (intersect s1 (cdr s2)))
) ;end cond
) ; end let
) ;end if
) ;end define
We can test for the equality of sets under the ordered list representation very simply - if they are equal as sets they must be equal as lists.
(define equal_set? equal?)
Note that intersect is an example of a general kind of operation, the merge in which two ordered sequences are compared in lock-step to produce a result derived from both of them. This is a very important kind of algorithm in cases in which you have large sets of data and only have sequential access to them. It past years, the only way that large data-sets could be stored was on magnetic tape, and all commercial data-processing depended on the use of merging operations. For example a bank would have records of the balance of customer accounts on one (or more than one!) tape, kept in order of account-number. The transactions for the day would be put on another tape, also in order of account-number. Then the two tapes would be merged, thereby updating the balances to allow for the transactions. Even the process of preparing the sorted-tape for merging would take place using a merge-based sorting operation.
Now we can test out our implementation.
(test_laws_sets 100)
If we represent a set as a balanced tree we can achieve a significant speed up in evaluating the member_set? and adjoin functions. The idea of a balanced tree is illustrated below - essentially the idea is that we want to equalise the number of entries to the left and right of each node as far as practicable.
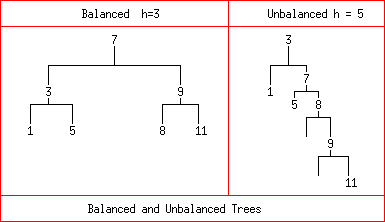
If a tree is balanced, we can get to any given node in a rather small number of steps, in fact in a number of steps logarithmic in the cardinality (size) of the set represented in the tree. The details of how we can achieve this are discussed in Lecture 15.