 x.E1)E2
x.E1)E2
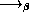 E1[x:=E2]
E1[x:=E2]
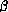 -reduction in terms of
substituting an argument given
to an abstraction for the variable of the abstraction in the body of the
abstraction, or, symbolically,
-reduction in terms of
substituting an argument given
to an abstraction for the variable of the abstraction in the body of the
abstraction, or, symbolically,
 x.E1)E2
x.E1)E2
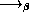 E1[x:=E2]
E1[x:=E2]
 x . * x 7) 22)
x . * x 7) 22) 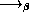 (* 22 7)
(* 22 7)
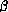 reduction as leaving the
expression (
reduction as leaving the
expression ( x.E1)E2
unchanged (or in other words, the reduced form "means the same thing" as
the original. Indeed, in the example above, we would like to claim that the
expression (sorted (merge_sort l)) means the same thing as the
expression true.
However, equality is a reflexive relation.
x.E1)E2
unchanged (or in other words, the reduced form "means the same thing" as
the original. Indeed, in the example above, we would like to claim that the
expression (sorted (merge_sort l)) means the same thing as the
expression true.
However, equality is a reflexive relation. 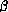 -reduction
isn't of course reflexive, but we can start constructing a closure
around it by considering the inverse operation to
-reduction
isn't of course reflexive, but we can start constructing a closure
around it by considering the inverse operation to
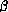 -reduction,
which we'll call
-reduction,
which we'll call 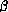 abstraction. We'll write the arrow the other
way round to indicate abstraction.
abstraction. We'll write the arrow the other
way round to indicate abstraction.
 x . * x 7) 22)
x . * x 7) 22)  (* 22 7)
(* 22 7)
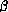 -conversion. For example:
-conversion. For example:
 x . * x 7) 22)
x . * x 7) 22)  (* 22 7)
(* 22 7)
 ((
(( x . * x 7) 22)
x . * x 7) 22)
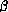 -rule is involved we'll
subscript the arrow with a
-rule is involved we'll
subscript the arrow with a 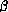 .
??? we need equivalence here
.
??? we need equivalence here
 -calculus. But a given expression may present several opportunities for applying reduction rules in
different places. To find out how to ensure that the result of a computation is
uniquely defined, we study normal forms and normal-order
reduction.
The
-calculus. But a given expression may present several opportunities for applying reduction rules in
different places. To find out how to ensure that the result of a computation is
uniquely defined, we study normal forms and normal-order
reduction.
The 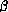 ,
, 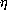 and
and 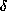 -reductions
which
we have considered can, in general, be applied in various places in an
expression. Consider, for example: (
-reductions
which
we have considered can, in general, be applied in various places in an
expression. Consider, for example: ( x.(+ 1
x))((
x.(+ 1
x))(( x.x)2). This can be reduced using
x.x)2). This can be reduced using 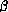 - reduction to (
- reduction to ( x.(+ 1 x))2 or
to + 1 ((
x.(+ 1 x))2 or
to + 1 (( x.x)2). Another stage of
x.x)2). Another stage of 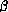 - reduction arrives at + 1 2 in both cases. In this
section we ask `does it matter where we chose to do the reduction'.
If E is an expression of
- reduction arrives at + 1 2 in both cases. In this
section we ask `does it matter where we chose to do the reduction'.
If E is an expression of  -calculus then a
redex is a
sub-expression of E which can be reduced by one of our rules.
-calculus then a
redex is a
sub-expression of E which can be reduced by one of our rules.
 x. x x)(
x. x x)( x.x x)
x.x x)

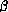 (
( x. x x)(
x. x x)( x.x x)
x.x x)
 expression can be rewritten forever to itself using
expression can be rewritten forever to itself using
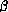 -reduction. Worse, consider:
-reduction. Worse, consider:
 x. x x x)(
x. x x x)( x.x x x)
x.x x x)

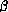 (
( x. x x x)(
x. x x x)( x.x x x)(
x.x x x)( x.x x x)
x.x x x)
 expression that gets bigger and bigger every time
it is rewritten. It should not surprise us that we might have difficulty in
telling whether a sequence of reductions in the
expression that gets bigger and bigger every time
it is rewritten. It should not surprise us that we might have difficulty in
telling whether a sequence of reductions in the  -calculus will terminate. If the
-calculus will terminate. If the
 -calculus is powerful enough to be a general purpose programming language, then
it is powerful enough
-calculus is powerful enough to be a general purpose programming language, then
it is powerful enough
If  is a relation, then we say that
is a relation, then we say that
 *
is the
transitive and reflexive closure of
*
is the
transitive and reflexive closure of  .
The * is often called
the Kleene Star operation, after the mathematician Kleene.
.
The * is often called
the Kleene Star operation, after the mathematician Kleene.
Formally,  *x,
and if x
*x,
and if x  y and y
y and y  *z
then x
*z
then x  * z.
* z.
Our reduction rules can be turned into conversion rules by taking the symmetric closure.
 E2
iff E1
E2
iff E1  E2 or
E2
E2 or
E2  E1
E1
Now we have shown that  *
is an infinite relation, since
we have exhibited a series of `reductions' a each step of which we obtain
a bigger expression \ref{blowup}. In navigating this infinite maze of
reduction, is there any guiding light, and can we recover if we take a
wrong turn? The answers are ``Yes! and Yes!'', as is shown by the
following:
*
is an infinite relation, since
we have exhibited a series of `reductions' a each step of which we obtain
a bigger expression \ref{blowup}. In navigating this infinite maze of
reduction, is there any guiding light, and can we recover if we take a
wrong turn? The answers are ``Yes! and Yes!'', as is shown by the
following:
 -calculus is said to be in
normal form if there is no expression E' for which E
-calculus is said to be in
normal form if there is no expression E' for which E E'.
E'.
For example
might be reduced to
or to
 E2 then there exists an expression E such that
E1
E2 then there exists an expression E such that
E1 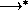 E and E2
E and E2 E
Corollary: A normal form for an expression is unique.
The strategy of always choosing to reduce the leftmost outermost redex
first always produces a normal form if one exists. This is called normal
order reduction.
E
Corollary: A normal form for an expression is unique.
The strategy of always choosing to reduce the leftmost outermost redex
first always produces a normal form if one exists. This is called normal
order reduction.
 E2 and E2 is a normal form, then normal order
reduction will always result in reduction to E2.
E2 and E2 is a normal form, then normal order
reduction will always result in reduction to E2.
This result is of great importance to the design of programming languages because it implies that the vast majority of programming languages (including Scheme and ML) are wrong!, because they do not use a normal order reduction. A small set of languages, of which Haskell is the most important, do use normal order reduction, or reductions that are provably equivalent to it.
For example the fraction-forms 3/4 and 6/8 ought to be the same but are constructed differently. So when we build the rational numbers we require each rational number to be a class of fraction-forms equivalent under the relation p/q == r/s iff ps=qr.
For this to work correctly, the relation which formally encodes "ought to be the same" must be an equivalence relation, that is to say it must be reflexive, symetric and transitive.
There is an additional requirement that applies to any operations that we want to define on the rationals, such as addition or multiplication. If these are to be functions, then we have to show that 6/8 + 2/14 == 3/4 + 1/7