Computer Science 591i
Rules of Inference

Basic Rules of Inference

[This owes much to the HOL system]

We said earlier that Theorem is a datatype that contains only "correct" theorems. In this section we consider the basic ways in which we can construct new theorems. Following HOL we capitalise the names of the functions which do this.

Recall that each theorem is of the form premises |- conclusion where premises is a list of terms, and conclusion is a term.

What exactly is the nature of theorems, and what's their relation to our programs? In a way, there is only an accidental relationship - we have created the Term datatype that lets us create objects that resemble those from which our programs are built. But, unlike classic LISP, there is no built-in eval function that couples these abstract syntactic structures to the execution mechanism of the language. So The Language lets us manipulate terms and theorems whose subject matter is the -calculus in much the same way as Mathematica lets us manipulate data-structures whose subject-matter is algebraic.

However, the Theorem datatype acts as a kind of contract between the language implementor and the language user. That is to say, if a user can create a theorem which says that his program should behave in one way, while the program actually behaves in another, then he has a rock-solid case for going to the implementor and saying that her implementation is broken. [Readers are invited to choose a permutation of the genders in the previous sentence to render it minimally sexist].

We characterise rules of inference with "vertical productions".

These indicate how one theorem is to be derived from one or more others. They typically have the form 
        theorems_before
        _____________

        theorem_after
However this characterisation achieves clarity by the suppression of detail. Many rules allow us to introduce a statement about an arbitrary term, which must be specified to make a rule algorithmically complete.

Rules are realised as functions available in The Language (but not, primitively, written in it) which typically map theorems_before and some additional member of Term into theorem_after.

When we state that the implementation of a rule may raise an exception, we mean that it is at the discretion of the implementor whether this is done. In this we differ radically from HOL; in that system type is integrated closely into the logic. In our case the type-system is simply a critic.

Rules which relate to Propositional Logic.

Our rules fall into various classes. Firstly there are those which interface between propositional logic and theorems. Now we've stated that a theorem has the form

What we may wonder is the difference between this theorem and the term where ==> is the implication operator of Propositional Logic, as encoded in our formalism? It helps to see an analogy here with Linear Algebra. In Linear Algebra we learnt to treat systems of linear equations such as 
        2x + 3y = 10
        3x + 7y = 8
using matrices such as 
       ( 2   3 )
       ( 3   7 )
The matrix is a convenient packaging of the original equations for the purpose of solution. Likewise, the theorem is a convenient packaging of statements first expressed using the Propositional connectives to say things about expressions in the -calculus.

So, our first group of proof-rules form an interface between theorems and the Propositional Calculus.

Rule 1: We may introduce an assumption

We may think of this as a way of encoding the tautology t==>t in theorem form.

ASSUME : Term -> Theorem 

      __________

        t |- t
ASSUME t evaluates to the theorem t |- t

For example ASSUME 'x=2' evaluates to the theorem 

    x=2 |- x=2
An implementation may raise an exception if the type of t in the current type environment is not Boolean.

Rule 2: Discharging an Assumption

This allows us to perform a step of conversion back from the Theorem form to a Propositional Calculus form. We can remove a specified term from the premises of a theorem and use it as the premise of a propositional implication from which the conclusion of the original theorem follows.

DISCH : Term -> Theorem -> Theorem 

                  |-  t2
                _________________________

                 - {t1} |- t1 ==> t2

Note that there's no need for t1 to be a member of 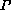. In this case 

   -{t1} =
For example (DISCH 'x=2' (ASSUME 'x=2')) evaluates to

(DISCH t1) may raise an exception if t1 is not of type Boolean in the current type environment.

Rule 3: Modus Ponens

MP: Theorem -> Theorem -> Theorem 

  1 |- t1 ==> t2        2 |- t1
  ___________________________

          1  2  |- t2
Thus (MP thm1 thm2) evaluates to a theorem obtained by applying the Modus Ponens rule as specified above. MP raises an exception if either of its arguments is not a theorem, or if the conclusion of the first argument is not an implication.

Rules which specify general facts about equality

Rule 4: Equality is reflexive

REFL : Term -> Theorem 
    ______________

      |-  t = t

Rule 5: Substituting Equal Terms

SUBST1 : Theorem -> Symbol -> Term -> Theorem -> Theorem 
    1 |- t1=t2       t[t1]
    ___________________________________

    1      |- t[t2]
Here t[t1] means "a term t with some occurrences of t1 singled out (for replacement)".

This is the most complicated rule. It embodies the general notion that entities that are equal ought to be interchangeable, so that if, say, t1=t2 then we ought to be able to replace t1 by t2 in any other term without changing its meaning. So, for example, if we have a theorem |- x*1 = x , and we have another theorem 

    |-  5*(x*1+6) = 5*(x*1) + 5*6
then we should be able to conclude that 
    |- 5*(x*1+6) = 5*x + 5*6
Notice that we have only replaced one occurrence of x*1 by x. Going back to considering exactly what SUBST1 does, we can say that the Symbol and Term arguments support the "singling out" process. Suppose we call 
    (SUBST1 thm1  v  ttem  thm)
Where thm1 has the f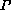orm |- t1 = t2 and thm has the form 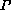|- t . Then ttem should be equal to t except that certain occurrences of t1 have been replaced by v (which variable will not normally occur in the theorems). Then exactly those occurrences of t1 which are "marked out" by v will be replaced by t2 in the new theorem.

The SUBST rule raises an exception when any of its arguments fails to have the right form.

[Note - HOL provides a more complicated rule, SUBST. We can write SUBST using SUBST1, although it will be distinctly less efficient].

Rules which are -calculus specific.

The remaining inference-rules encode the -reduction rule and say that the -abstraction of equal terms gives equal abstractions.

Rule 6: Beta-conversion

BETA : Term -> Theorem 
     ____________________________

       |- (\x.E1)E2 = E1[x:=E2]
The argument t of (BETA t) must have the form of a -abstraction applied to an argument. If so, -reduction is performed as specified previously, and the original and -reduced forms are equated.

If the term t is not a -redux [i.e. is not of the form specified] an exception is raised.

For example: (BETA '(\x. 5+x) 20') evaluates to 

    |-  (\x. 5+x) 20 = 5 + 20

Rule 7: Abstraction

ABS : Symbol -> Theorem -> Theorem

The abstraction rule allows us infer the the equality of abstractions from the equality of terms. 

              |- t1 = t2
        _________________________

         |- (\x. t1) = (\x. t2)

Provided x does not occur free in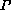

Example: ABS 'x' (REFL 'v') evaluates to 
        |- \x.v = \x.v
The call (ABS v) raises an exception if v occurs free in any assumption in .

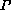But We Build Mightily Upon These Rules

The above inference rules are the "car, cdr, cons of program verification. The list-constructors of LISP and its descendants police the use of memory so that users can't create illegal structures (pointers to nowhere etc.) However one doesn't (or shouldn't) write programs that create complex data-structures using just car, cdr, cons, but should instead create levels of abstraction using these primitives.

Likewise we are free to write functions that manipulate theorems knowing that the only theorems we can create are provably correct (since we can create a proof of any theorem from the system axioms by following the sequences of inference-rule applications).

Looking inside theorems

In fact the proof-rules are in effect abstract constructors for theorems, and play the role of cons in LISP. There's no harm in looking inside a theorem. This is supported as follows: 
Theorem.? : Top->Boolean           Recognises if an object
                                   is a theorem

Theorem.hyp : Theorem->List(Term)  Extracts the list of
                                   hypotheses

Theorem.concl: Theorem->Term       Extracts the conclusion

Theorem.history: Theorem->History  Extracts the inference history of
                                   the theorem.

Theorem.add_history:               Makes a new theorem with an
        Theorem->History->Theorem  appropriate history.
The "add_history" capability calls for comment. It is an exception to the rule that users can only create theorems using proof-methods. In effect, it allows a user to rewrite the history of a theorem. While this may appear to have Stalinist potential, it primarily serves to allow useful histories to be created by higher-level theorem-manipulating functions. The inference-rules operate at a very fine grain, and it makes sense for higher level functions to be able to suppress details of this fine-grain operation in the historical record.

Writing a Derived Inference Rule

As an example, let's write a new inference rule, 
    ADD_ASSUME : Term -> Theorem -> Theorem
(ADD_ASSUME t1 thm) simply adds the (redundant) assumption t1 to the existing assumptions of the theorem. So it embodies a new rule: 
        |-  t
    ______________

    , t1  |- t
We can realise this rule with the following definition: 
Definition ADD_ASSUME =
    \ t1 thm.                       ;;; thm = G |- t, say
        let thm1 = ASSUME t1,       ;;; t1 |- t1
            thm2 = DISCH t1 thm,    ;;; G  |- t1==>t
        in
            MP thm2 thm1            ;;; G,t1 |- t
        endlet
End;