 -calculus down?
-calculus down? -calculus down?
-calculus down?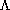 (D) which are syntactically distinct. For example
(D) which are syntactically distinct. For example
 x. (+ x a)) p)
x. (+ x a)) p)
From now on we'll write
(d1 d2)
for 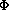 (d1)(d2).
(d1)(d2).
 ,
,
 [
[
 x1 . . . xn. d]
(
x1 . . . xn. d]
(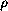 )
)
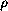 ,
,
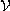 [
[
 x1 . . . xi . . .
xn. xi]
(
x1 . . . xi . . .
xn. xi]
(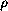 )
)
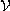 [
[
 x1 . . . . xn . x1]
(
x1 . . . . xn . x1]
(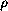 )
)
= 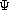 (f)
(f)
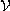 [
[
 x2 . . . . xn . x1]
(
x2 . . . . xn . x1]
(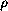 [x1:=d])
[x1:=d])
= 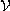 [
(
[
( x2 . . . . xn .
x1) [x1:=d]
(
x2 . . . . xn .
x1) [x1:=d]
(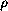 )
)
= 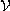 [
(
[
( x2 . . . . xn . d)]
(
x2 . . . . xn . d)]
(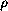 )
)
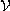 [
[
 x1 . . . xi . . .
xn. xi]
(
x1 . . . xi . . .
xn. xi]
(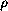 )
)
Consider
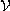 [
[
 x1 . . . xi+1 . . .
xm. xi+1]
(
x1 . . . xi+1 . . .
xm. xi+1]
(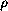 ) =
) = 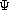 (f)
(f)
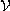 [
[
 x2 . . . . xn . xi+1]
(
x2 . . . . xn . xi+1]
(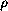 [x1:=d])
[x1:=d])
= 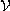 [
(
[
( x2 . . . . xn .
xi+1) [x1:=d]
(
x2 . . . . xn .
xi+1) [x1:=d]
(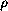 )
)
= 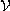 [
(
[
( x2 . . . . xn .
xi+1)] [x1:=d]
(
x2 . . . . xn .
xi+1)] [x1:=d]
(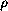 )
)
= 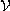 [
(
[
( x2 . . . . xn .
xi+1)]
(
x2 . . . . xn .
xi+1)]
(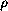 )
)
= (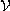 [
(
[
( x2 . . . . xn .
xi+1)]
(
x2 . . . . xn .
xi+1)]
(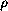 ) d2 . . .dn)
) d2 . . .dn)
= di+1
 x1 . . . xn . xi
=
x1 . . . xn . xi
=  x1 . . . xn . xj
x1 . . . xn . xj
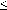 i < j
i < j 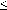 n
is not valid in any environment model
n
is not valid in any environment model 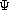
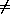 dj
and apply lemma EM5.
dj
and apply lemma EM5.
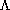 (C)
has a corresponding combinatory lambda term E' which is
alpha-beta equivalent to it. We also showed that any applicative
algebra which was the image of
(C)
has a corresponding combinatory lambda term E' which is
alpha-beta equivalent to it. We also showed that any applicative
algebra which was the image of 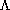 (C) under
a valuation necessarily contained the combinators S,K,I.
(C) under
a valuation necessarily contained the combinators S,K,I.
Now in considering environment models, we have already adopted the
convention that we write (d1 d2) for
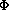 (d1)(d2). This immediately
raises the idea, could we get an environment model from a combinatory
algebra by defining
(d1)(d2). This immediately
raises the idea, could we get an environment model from a combinatory
algebra by defining
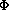 (d1)(d2)
= (d1
(d1)(d2)
= (d1 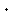 d2)
d2)
Unfortunately the axioms for a combinatory algebra aren't quite strong
enough for this to work, because we also need the 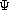 function, which is a left-inverse of
function, which is a left-inverse of 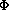 . Let's consider
the function which maps d to
. Let's consider
the function which maps d to
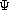 (
(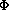 (d)). Indeed, let's suppose
it is a function which corresponds to an element
(d)). Indeed, let's suppose
it is a function which corresponds to an element
e  D. Then we have
D. Then we have
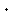 d0)
d0) 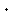 d1
d1
= (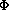 (
(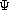 (
(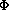 (d0)))
(d0))) 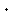 d1)
d1)
= (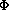 (d0)
(d0) 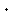 d1)
= (d0
d1)
= (d0 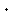 d1)
d1)
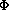 is the left inverse of
is the left inverse of 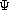 .
.