EX1 (
(
 d) =
d) =  for
for 

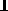
EX2 (d
(d 
 ) =
) =  for
for 

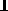
The utility of type models is that they are smaller than models in which a general computation can be supported. This means that they can serve a useful purpose in predicting whether an error will occur.
In Computer Science, types serve two major purposes:
In their first role, type-systems can be regarded as a kind of weak logic, capable of inferring that certain events, called type-errors cannot occur. The most important property of a type system is that type-correctness of a program must be decidable. From this requirement, it is clear that not all errors are type-errors, since failure of a program to terminate should clearly be regarded as an error, but the halting problem is undecidable.
If we want to examine the idea of a type-system from the point of view of Combinatory Models, the natural approach is to introduce the idea of a set of exceptions in the model. If an expression can evaluate to an exception, then it should be regarded as erroneous.
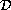 = <D,
= <D, 
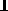 >
>
EX1 (
(
 d) =
d) =  for
for 

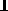
EX2 (d
(d 
 ) =
) =  for
for 

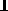
 1
1 
 2)
=
2)
=  1.
1.
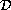 =
<D,
=
<D, ,S, K,
,S, K, 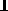 >
which is an applicative algebra with exceptions, and
where S, K are Shonfinkel combinators obeying:
>
which is an applicative algebra with exceptions, and
where S, K are Shonfinkel combinators obeying:
K c x = c
S f g x = (f x) (g x)
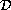 be a combinatory algebra, with exception set
be a combinatory algebra, with exception set 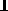 . We say that p in
. We say that p in 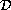 is
a procedure if for some
d
is
a procedure if for some
d  |
| 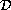 |
, the application (p
|
, the application (p  u)
is not in
u)
is not in 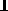 .
.
We denote the type of procedures of  by Proc(
by Proc( ).
).
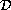 be an applicative algebra. Then a type
T
be an applicative algebra. Then a type
T
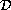 is a subset of
is a subset of
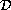 .
.
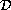 is a combinatory model
and TD and TR are types of
is a combinatory model
and TD and TR are types of 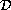 , then
TD
, then
TD TR is the type
TR is the type
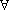 d', d'
d', d'  TD
TD
 (d
(d  d')
d')  TR }
TR }
If d 
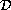 ,
we say that d has the (weak) type
TD
,
we say that d has the (weak) type
TD  TR if
d
TR if
d  TD
TD  TR.
TR.
It should be noted that given our existing type-descriptive
apparatus
no unique procedure-type can be ascribed to a procedure. For a
given procedure object d it is possible that p  TD1
TD1  TR1 and also p
TR1 and also p
 TD2
TD2  TR2
where there is way of expressing these two relationships in the form of
p
TR2
where there is way of expressing these two relationships in the form of
p  TD3
TD3  TR3
without losing useful discriminatory power. For example, the absolute
value procedure in the FSM has among its types:
TR3
without losing useful discriminatory power. For example, the absolute
value procedure in the FSM has among its types:
 Integer
Integer  Integer
Integer  Number
Number  Number
Number
But the second of these statements does not subsume the first, because the first statement tells us the relevant fact that if we give abs an integer as argument it returns an integer as result.
If TD1, TD2, TR1, TR2,
are types for which
TD2  TD1 and
TR1
TD1 and
TR1  TR2,
then
TR2,
then
 TR1
TR1
 TD2
TD2  TR2
TR2
Let p  TD1
TD1  TR1 .
Then (p
TR1 .
Then (p  d1)
d1)
 TR1
for all d1
TR1
for all d1  TD1 .
TD1 .
But TD2  TD1. Hence
for all
d2
TD1. Hence
for all
d2  TD2,
(p
TD2,
(p  d2)
d2)
 TR1.
Since however TR1
TR1.
Since however TR1  TR2 ,
we see that
(p
TR2 ,
we see that
(p  d2)
d2)  TR2 .
TR2 .
Thus we have shown that any
p  TD1
TD1  TR1
maps TD2 to TR2, thus establishing our lemma.
TR1
maps TD2 to TR2, thus establishing our lemma.
A consequence of the contravariance rule is that, for example, despite
the fact that Integer  Number, the type
Integer
Number, the type
Integer  Integer is not contained in
the type Number
Integer is not contained in
the type Number  Number. Thus, for
example, the intersection
Number. Thus, for
example, the intersection
 Integer)
Integer)
 (Number
(Number  Number)
Number)
is non-redundant.
A simple converse of these two lemmas is clearly not true of all combinatory algebras.
for consider a combinatory algebra without procedure objects. Then
TD TR is always the empty-set for
any TR which contains no exceptions, so that
TD1
TR is always the empty-set for
any TR which contains no exceptions, so that
TD1  TR1
TR1  TD2
TD2  TR2 is true for any combinatory algebras and ranges
whatever.
TR2 is true for any combinatory algebras and ranges
whatever.
Since the combinators are denizens of every combinatory algebra, let's start with their type.
 T
T T
T
Let t  T. Then
I
T. Then
I  t
= t. Thus I
t
= t. Thus I  T
T T.
T.
 T1
T1  T2
T2
 T1
T1
 T1, consider
(K
T1, consider
(K  t1). For all t2
t1). For all t2  T2,
(K
T2,
(K  t1)
t1)  t2 = t1. Thus
(K
t2 = t1. Thus
(K  t1)
t1)  T2
T2  T1. Hence K
T1. Hence K  T1
T1  (T2
(T2  T1)
T1)
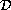 where
T'2
where
T'2  T2 ,
then
T2 ,
then
 (T1
(T1  T2
T2  T3)
T3)  (T1
(T1  T'2)
T'2)  T1
T1  T3
T3
It is sufficient to show that if f  T1
T1  T2
T2
 T3
then (S
T3
then (S  f)
f)  (T1
(T1  T'2)
T'2)
 T1
T1
 T3
T3
Hence it suffices to show that if, in addition, g  T1
T1  T'2 then
(S
T'2 then
(S  f
f  g)
g)
 T1
T1  T3 .
T3 .
Hence it suffices to show that if, in addition,
x  T1 then
S
T1 then
S  f
f  g
g  x
x  T3 .
T3 .
But S  f
f  g
g  x = (f
x = (f  x)
x)  (g
(g  x). Since x
x). Since x  T1 , and f
T1 , and f
 T1
T1  T2
T2
 T3 , it follows that (f
T3 , it follows that (f  x)
x)
 T2
T2  T3.
Likewise (g
T3.
Likewise (g  x)
x)  T'2.
But
T'2
T'2.
But
T'2  T2 ,
so that ((f
T2 ,
so that ((f  x)
x)  (g
(g  x))
x))  T3 . Hence
(S
T3 . Hence
(S  f
f  g
g  x) in T3 ,
hence (S
x) in T3 ,
hence (S  f
f  g) in
T1
g) in
T1  T3 ,
hence (S
T3 ,
hence (S  f)
f)  (T1
(T1  T'2)
T'2)
 T1
T1
 T3 ,
hence
T3 ,
hence
 (T1
(T1  T2
T2
 T3)
T3) (T1
(T1  T'2
)
T'2
)  T1
T1
 T3
T3
One interpretation of the above results is that a particular type for one of the combinators is as an intersection. For example, for any two types T1 and T2:
 (T1
(T1  T1)
T1)
 ( T2
( T2  T2)
T2)
And in general, for any family (Tj) of types:

 j
j  J
( Tj
J
( Tj  Tj)
Tj)
 ) of the algebra. This allows the algebraist to
project the original algebra onto a quotient algebra,
which she hopes will be sufficiently simple to allow her to make useful
predictions about the big algebra.
) of the algebra. This allows the algebraist to
project the original algebra onto a quotient algebra,
which she hopes will be sufficiently simple to allow her to make useful
predictions about the big algebra.
This is quite easily realised in a simple applicative algebra. For
example, consider an algebra which has the Scheme integers and floats,
together with the abs procedure, which takes the absolute
value of a number. Then
we can take Integer,
Float, {abs}, 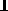 as separate types, obtaining a finite applicative algebra:
as separate types, obtaining a finite applicative algebra:
(Integer  Integer) =
Integer) = 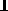
(Integer  Float) =
Float) = 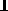
(Float  Float) =
Float) = 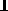
(Float  Integer) =
Integer) = 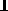
({abs}  Integer) = Integer
Integer) = Integer
({abs}  Float) = Float
Float) = Float
({abs}  {abs}) =
{abs}) = 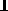
A projection mapping 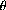 always induces a partition of its
domain into pairwise disjoint sets whose union is the whole domain.
always induces a partition of its
domain into pairwise disjoint sets whose union is the whole domain.
 = <D,
= <D,  >,be a
applicative
algebra.
Suppose we have a family of types
T1, T2, . . . which form a partition
of D, that is, they are non-empty, pairwise disjoint
[that is Ti
>,be a
applicative
algebra.
Suppose we have a family of types
T1, T2, . . . which form a partition
of D, that is, they are non-empty, pairwise disjoint
[that is Ti  Tj =
Tj = 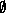 for
all i
for
all i 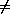 j] and the union
T1
j] and the union
T1  T2, . . . = D . Suppose also
that, for all Ti
T2, . . . = D . Suppose also
that, for all Ti
 d, d'
d, d'  Ti
Ti  (
(
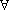 p
p  D,
(p
D,
(p  d)
d)  Tj
Tj
 (p
(p  d')
d')  Tj)
Tj)
 p, p'
p, p'  Ti
Ti  (
(
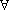 d
d  D,
(p
D,
(p  d)
d)  Tj
Tj
 (p'
(p'  d)
d)  Tj)
Tj)
 .
.
 = <D,
= <D, >
be an applicative algebra with a congruence partition
T1, T2, . . ..
Define (Ti
>
be an applicative algebra with a congruence partition
T1, T2, . . ..
Define (Ti  Tj) to be
Tk where for some
ti
Tj) to be
Tk where for some
ti  Ti,
tj
Ti,
tj  Tj we have
(ti
Tj we have
(ti  tj)
tj)  Tk. Then the types
T1, T2, . . ..
form an applicative algebra.
Tk. Then the types
T1, T2, . . ..
form an applicative algebra.
 operation on the
types is well defined.
operation on the
types is well defined.
Let ti, t'i  Ti
and
tj, t'j
Ti
and
tj, t'j  Tj
Let (ti
Tj
Let (ti  tj)
tj)  .
Tk. Then (ti
.
Tk. Then (ti  t'j)
t'j)  Tk by HM1, and hence
(t'i
Tk by HM1, and hence
(t'i  t'j)
t'j)  .
Tk by HM2. Thus the
.
Tk by HM2. Thus the  operation is
well-defined.
operation is
well-defined.
Given a congruence partition of an applicative algebra, where
d Ti
we write [[d]] for Ti. Thus from
definition CP we see that
Ti
we write [[d]] for Ti. Thus from
definition CP we see that
 [[d2]]) =
[[(d1
[[d2]]) =
[[(d1  d2)]]
d2)]]
Suppose our applicative algebra is a combinatory algebra. Then it is easy enough to extend the above lemma to show that a congruence partition of our combinatory algebra is itself a combinatory algebra. Since K and S are defined equationally, the following lemma is an instance of a well known theorem of Universal Algebra. However, we give here an elementary proof.
 = <D,
= <D, , S, K>
be a combinatory algebra with a congruence partition
T1, T2, . . .. Then the
types of the partition form a combinatory algebra under the
operation defined above.
, S, K>
be a combinatory algebra with a congruence partition
T1, T2, . . .. Then the
types of the partition form a combinatory algebra under the
operation defined above.
 [[d1]]
[[d1]]  [[d2]]) =
[[(K
[[d2]]) =
[[(K  d1
d1  d2)]] = [[d1]]
d2)]] = [[d1]]
([[S]]  [[d1]]
[[d1]]  [[d2]]
[[d2]]  [[d3]]) =
[[(S
[[d3]]) =
[[(S  d1
d1  d2
d2  d3) ]]
d3) ]]
= [[(d1  d3)
d3)  (d2
(d2  d3) ]]
= [[((d1
d3) ]]
= [[((d1  d3)
d3)  (d2
(d2  d3))]]
d3))]]
= (([[d1]]  [[d3]])
[[d3]])
 ([[d2]]
([[d2]]  [[d3]]))
[[d3]]))
To extend these ideas to a combinatorial model we need to meet the
" conditions" of the combinatory model. But these are not
equational, and so are not automatically satisfied by the
idea of congruence as defined, just as for example the quotient
of an integral domain by an ideal is not necessarily an integral domain.
Saying "there are no divisors of zero" is not an equational statement.
Thus while the integers form an integral domain, the ring of integers
modulo six has divisors of zero, namely [[3]] and [[2]].
conditions" of the combinatory model. But these are not
equational, and so are not automatically satisfied by the
idea of congruence as defined, just as for example the quotient
of an integral domain by an ideal is not necessarily an integral domain.
Saying "there are no divisors of zero" is not an equational statement.
Thus while the integers form an integral domain, the ring of integers
modulo six has divisors of zero, namely [[3]] and [[2]].
We can approach this problem from another point of view. Let's introduce the idea of monomorphic procedure types
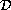 is an applicative algebra with exceptions,
and TD and TR are types of
is an applicative algebra with exceptions,
and TD and TR are types of 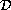 , then the monomorphic procedure
type TD
, then the monomorphic procedure
type TD TR is the type
TR is the type
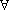 d', d'
d', d'  TD
TD
 (d
(d  d')
d')
 TR
& d'
TR
& d'  TD
TD
 (d
(d  d')
d')

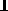 }
}
The concept is of course too restrictive to serve to characterise
all of the types of SML procedure, which are parametrically
polymorphic. It' also too restrictive to characterise the
S, K, I combinators which are likewise parametrically polymorphic.
But it does give us a start in letting us create an applicative algebra
of types with a simple definition of the
also too restrictive to characterise the
S, K, I combinators which are likewise parametrically polymorphic.
But it does give us a start in letting us create an applicative algebra
of types with a simple definition of the  operator, and
which is extensional with respect to its procedure-types.
operator, and
which is extensional with respect to its procedure-types.
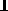 , T1,
T2, . . .) if the Ti are either
monomorphic procedure types or consist of non-procedures.
, T1,
T2, . . .) if the Ti are either
monomorphic procedure types or consist of non-procedures.
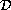 be a partitioned applicative algebra.
Then, if TD, TR and (TD
be a partitioned applicative algebra.
Then, if TD, TR and (TD  TR)
are members of the partition,
((TD
TR)
are members of the partition,
((TD  TR)
TR)  TD) = TR.
TD) = TR.
 d)
d)  ((TD
((TD  TR)
TR)  TD), where p
TD), where p  (TD
(TD  TR).
Hence (p
TR).
Hence (p  d)
d)  TR. But, by
definition of application in the quotient algebra, ((TD
TR. But, by
definition of application in the quotient algebra, ((TD  TR)
TR)  TD) is a member of
the partition, as is TR, by hypothesis.
Hence, having p
TD) is a member of
the partition, as is TR, by hypothesis.
Hence, having p  d in common, they are
the same member of the partition.
d in common, they are
the same member of the partition.
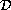 be a monomorphically partitioned applicative algebra.
Suppose for all T in the partition
be a monomorphically partitioned applicative algebra.
Suppose for all T in the partition
 TR1)
TR1)
 T) =
((TD2
T) =
((TD2  TR2)
TR2)
 T)
T)
 TR1
and
TD2
TR1
and
TD2  TR2
are members of the partition as are the non-exceptional TD1,
TD2, TR1, TR2.
Then
TR2
are members of the partition as are the non-exceptional TD1,
TD2, TR1, TR2.
Then
 TR1)
=
(TD2
TR1)
=
(TD2  TR2)
TR2)
 TR2)
TR2)
 TD2) = TR2
= ((TD1
TD2) = TR2
= ((TD1  TR1)
TR1)
 TD2)
TD2)
 d)
d)  ((TD1
((TD1  TR1)
TR1)
 TD2) , where p
TD2) , where p  TD1
TD1  TR1,
d
TR1,
d  TD2.
Now p is a member of the monomorphic procedure type
TD1
TD2.
Now p is a member of the monomorphic procedure type
TD1  TR1
Hence d
TR1
Hence d  TD1, for TR2
contains no exceptions, and p raises an exception for every
argument not in TD1.
TD1, for TR2
contains no exceptions, and p raises an exception for every
argument not in TD1.
Thus TD1 and TD2 have an element in common, and being members of the partition, TD1= TD2
Also
p  d
d  TR1
and
p
TR1
and
p  d
d  TR2,
since .
d
TR2,
since .
d  TD1
and
d
TD1
and
d  TD2.
Thus
TR1, TR2 have an element in common, and
being members of the partition, TR1= TR2
TD2.
Thus
TR1, TR2 have an element in common, and
being members of the partition, TR1= TR2
Hence the result.
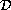 /(
/(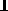 T1 . . .)
has part of the requisite extensional property to render it a combinatorial
model, assuming it contains the necessary combinators. However we have
problems still.
T1 . . .)
has part of the requisite extensional property to render it a combinatorial
model, assuming it contains the necessary combinators. However we have
problems still.
It is not hard to construct monomorphically partitioned applicative algebras
with a finite collection of procedure objects, and a finite partition.
But adding combinators gives rise to an infinite collection of procedure
objects, which require an extension of the idea of monomorphic functional types.
Consider for example, the I combinator. It can take as its argument
any object. However our requirement that objects be
partitioned into distinct types does not allow us to have the
idea of type-union, and indeed, a characterisation of I
in terms of type-union is too imprecise. For, while I has the (weak)
type TD  TD where TD is the
carrier set of
TD where TD is the
carrier set of  , this does not capture the fact that
I
, this does not capture the fact that
I  T
T  T for all types
T, that is to say, that
I
T for all types
T, that is to say, that
I 
 i
(Ti
i
(Ti  Ti)
for any family of types (Ti).
Ti)
for any family of types (Ti).