 -conversion (and other matters) is
going to occur. This is marked by the symbol
-conversion (and other matters) is
going to occur. This is marked by the symbolThis leaves us with the cases in which we have one path contained in another. We'll need to tuck a few more appropriate lemmas under our belt before we can essay the remaining cases.
We'll need to prove these using induction on path-length, so let's define this useful concept.
length(s::p) = 1+length(p)
Also, a certain amount of hand-waving with respect to  -conversion (and other matters) is
going to occur. This is marked by the symbol
-conversion (and other matters) is
going to occur. This is marked by the symbol


 P'
and Q
P'
and Q 
 Q'
and P
Q'
and P 
 Q
then
P'
Q
then
P'
 Q'
Q'
 Let E be a term of the
Let E be a term of the  -calculus, and let
p be a path. We say that p properly addresses
the term E if cases PH2, PH3 of the definition of the concept
of address by a path don't occur.
-calculus, and let
p be a path. We say that p properly addresses
the term E if cases PH2, PH3 of the definition of the concept
of address by a path don't occur.
 -calculus, with
v a variable, and let p be a path. We say that
v remains in scope from E down p, and write seen(v,E,p)
according to the following definition:
-calculus, with
v a variable, and let p be a path. We say that
v remains in scope from E down p, and write seen(v,E,p)
according to the following definition:
SC1 It is always the case that seen(v,E,())
SC2 Otherwise, if E = u, a variable, or E = c, a constant, then seen(v,E,p) holds.
SC3 Otherwise, if E = (F G), an application, then
SC3.1 If hd(p) = 0 then seen(v,E,p) iff seen(v,F,tl(p))
SC3.2 If hd(p) = 1 then seen(v,E,p) iff seen(v,G,tl(p))
SC4 Otherwise, if E =  v.G then it is
not the case that seen(v,E,p). In this case, we
say that v goes out of scope.
v.G then it is
not the case that seen(v,E,p). In this case, we
say that v goes out of scope.
SC5 Otherwise, if E =  u.G then
u.G then
SC5.1 If hd(p) = 0 then seen(v,E,p)
SC5.2 If hd(p) = 1 then seen(v,E,p) iff seen(v,G,tl(p))
 -calculus, and
v is a variable of the aforementioned, and p is a
path which properly addresses E
and seen(v,E,p) then there is an E' which is
-calculus, and
v is a variable of the aforementioned, and p is a
path which properly addresses E
and seen(v,E,p) then there is an E' which is
 -congruent to E for which
-congruent to E for which
 Let E' be formed from E by
Let E' be formed from E by  -converting
any
-converting
any  -abstraction found on p whose bound
variable is a member of FV(F) to an abstraction whose bound
variable is not a member of FV(F).
-abstraction found on p whose bound
variable is a member of FV(F) to an abstraction whose bound
variable is not a member of FV(F).
We now proceed by induction on the length of p.
 n implies that
n implies that
E'[p][v:=F] = C[p'][v:=F] = C[v:=F][p']
The last step above uses the inductive hypothesis, justified because length(p') = n, and seen(v,C,p') by SC3. On the other hand, using S5
Hence the result holds in this sub-case.
 x . H, an abstraction.
We have 2 sub-cases,
s=0 and s=1
x . H, an abstraction.
We have 2 sub-cases,
s=0 and s=1
 x . H)[p][v:=F]
= (
x . H)[p][v:=F]
= ( x . H)[v:=F]
x . H)[v:=F] x . H)[v:=F][p]
x . H)[v:=F][p]
Since substitution converts an abstraction into an abstraction. So the result holds for this sub-case.
E'[p][v:=F] = ( x . H)[p][v:=F]
x . H)[p][v:=F]
= H[p'][v:=F]
= H[v:=F][p']
using the inductive hypothesis. On the other hand, we have our very favourite can of worms when we come to
E'[v:=F][p]
because we have to consider cases S5-S7 of the definition of substitution.
In this sub-sub-case, v goes out of scope, so, by ex falsa libet the result holds.
 v
and either x
v
and either x  FV(F)
or v
FV(F)
or v  FV(H)
Here
FV(H)
Here
 x. H)[v:=F][p]
= (
x. H)[v:=F][p]
= ( x. H[v:=F])[p]
= H[v:=F][p']
x. H[v:=F])[p]
= H[v:=F][p']
So the result holds in this sub-sub-case
 v
and x
v
and x  FV(F)
or v
FV(F)
or v  FV(H)
FV(H)
This sub-case can't occur because of the way we have defined E'.
 -calculus, and
v is a variable of the aforementioned, and p is a
path which properly addresses E
and seen(v,E,p) then there is an E' which is
-calculus, and
v is a variable of the aforementioned, and p is a
path which properly addresses E
and seen(v,E,p) then there is an E' which is
 -congruent to E for which
-congruent to E for which
 Let E' be formed from E by
Let E' be formed from E by  -converting
any
-converting
any  -abstraction found on p whose bound
variable is a member of FV(F) to an abstraction whose bound
variable is not a member of FV(F).
-abstraction found on p whose bound
variable is a member of FV(F) to an abstraction whose bound
variable is not a member of FV(F).
We now proceed by induction on the length of p.
 n implies that
n implies that
E'[p:=G][v:=F] = (C[p':=G] D)[v:=F]
= (C[p':=G][v:=F] D[v:=F])
= (C[v:=F][p':=G[v:=F]] D[v:=F])
The last step above uses the inductive hypothesis, justified because length(p') = n, and seen(v,C,p') by SC3. On the other hand, using S5
= (C[v:=F][p':=G[v:=F]] D[v:=F])
Hence the result holds in this sub-case.
 x . H, an abstraction.
We have 2 sub-cases,
s=0 and s=1
x . H, an abstraction.
We have 2 sub-cases,
s=0 and s=1
 x . H)[p:=G[v:=F]][v:=F]
x . H)[p:=G[v:=F]][v:=F]
= ( x . H)[v:=F]
x . H)[v:=F]
= ( x . H)[v:=F][p:=G[v:=F]]
x . H)[v:=F][p:=G[v:=F]]
Since substitution converts an abstraction into an abstraction. So the result holds for this sub-case.
Now we again (sigh!) have to consider cases S5-S7 of the definition of substitution.
In this sub-sub-case, v goes out of scope, so, by ex falsa libet the result holds.
 v
and either x
v
and either x  FV(F)
or v
FV(F)
or v  FV(H).
Here
FV(H).
Here
 x . H)[p:=G][v:=F]
x . H)[p:=G][v:=F]
= ( x . H[p':=G])[v:=F]
= (
x . H[p':=G])[v:=F]
= ( x . H[p':=G][v:=F])
x . H[p':=G][v:=F])
= ( x. H[v:=F][p':=G[v:=F]])
x. H[v:=F][p':=G[v:=F]])
On the other hand,
 x. H)[v:=F][p:=G[v:=F]]
x. H)[v:=F][p:=G[v:=F]]
= ( x. H[v:=F])[p:=G[v:=F]]
x. H[v:=F])[p:=G[v:=F]]
= ( x. H[v:=F][p':=G[v:=F]])
x. H[v:=F][p':=G[v:=F]])
So the result holds in this sub-sub-case
 v
and x
v
and x  FV(F)
or v
FV(F)
or v  FV(H)
This sub-case can't occur because of the way we have defined E'.
FV(H)
This sub-case can't occur because of the way we have defined E'.
 -calculus, and
let u, v be variables,
for which u
-calculus, and
let u, v be variables,
for which u 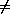 v
v FV(G) and
v
FV(G) and
v  FV(F). Let it be the case also
that no variable bound in E is free in F or in
G. Then
FV(F). Let it be the case also
that no variable bound in E is free in F or in
G. Then
Base Case n=0
By Lemma Sub.1, since v  FV(F).
FV(F).
On the other hand
So the result is satisfied for this case.
On the other hand
by Lemma Sub.1, since u  FV(G)
FV(G)
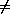 u,v
u,v
On the other hand
So the lemma holds in this case.
Suppose E = c  C.
C.
This case is similar to the preceding one.
Inductive Step
Suppose for a given n we have for any term E for which
height(E)  n
n
Consider an expression E of height n+1 We must show our result holds for E
.Using S4 repeatedly we obtain:
E[u:=F][v:=G] = (C D)[u:=F][v:=G]
= (C[u:=F] D[u:=F])[v:=G] = (C[u:=F][v:=G] D[u:=F][v:=G])
So using the inductive hypothesis.
= (C[v:=G][u:=F] D[v:=G][u:=F])
On the other hand,
(C[v:=G] D[v:=G])[u:=F]
= (C[v:=G][u:=F] D[v:=G][u:=F])
So the lemma holds in this case.
 u . H.
u . H.
E[u:=F][v:=G] = ( u . H)[u:=F][v:=G]
u . H)[u:=F][v:=G]
= ( u . H)[v:=G]
u . H)[v:=G]
= ( u . H[v:=G])
u . H[v:=G])
since u  G.
G.
On the other hand
 u . H)[v:=G][u:=F]
u . H)[v:=G][u:=F]
= ( u . H[v:=G])[u:=F]
u . H[v:=G])[u:=F]
= ( u . H[v:=G])
u . H[v:=G])
thus the lemma holds for this case.
 v . H.
v . H.
E[u:=F][v:=G] = ( v . H)[u:=F][v:=G]
v . H)[u:=F][v:=G]
= ( v . H[u:=F])[v:=G]
v . H[u:=F])[v:=G]
since v  FV[F]
FV[F]
= ( v . H[u:=F])
v . H[u:=F])
On the other hand
 v . H)[v:=G][u:=F]
v . H)[v:=G][u:=F]
= ( v . H)[u:=F]
= (
v . H)[u:=F]
= ( v . H[u:=F])
v . H[u:=F])
Since v  FV(F)
FV(F)
thus the lemma holds for this case.
 x . H
By the premises of this Lemma,
x
x . H
By the premises of this Lemma,
x  FV(F) and
x
FV(F) and
x  FV(G).
FV(G).
Hence
E[u:=F][v:=G] = ( x . H)[u:=F][v:=G]
x . H)[u:=F][v:=G]
= ( x . H[u:=F])[v:=G]
x . H[u:=F])[v:=G]
= ( x . H[u:=F][v:=G])
x . H[u:=F][v:=G])
= ( x . H[v:=G][u:=F])
x . H[v:=G][u:=F])
by the inductive hypothesis.
On the other hand
since
x  FV[F]
FV[F]
 FV[G] this
FV[G] this
 x . H)[v:=G][u:=F]
x . H)[v:=G][u:=F]
= ( x . H[v:=G])[u:=F]
x . H[v:=G])[u:=F]
= ( x . H[v:=G][u:=F])
x . H[v:=G][u:=F])
 u.C) G)
be a redex of the
u.C) G)
be a redex of the  -calculus.
-calculus.
Let p be a path for which
E[p] = ( v.D) H)
where hd(p)=0 and hd(tl(p))=1.
and also seen(u,E,p).
Let p' = tl(tl(p)). Then
v.D) H)
where hd(p)=0 and hd(tl(p))=1.
and also seen(u,E,p).
Let p' = tl(tl(p)). Then
 (
( (E,()),p')
(E,()),p')


 (
( (E,p),())
(E,p),())
 Let C' be formed from C by
Let C' be formed from C by  -converting
any
-converting
any  -abstraction whose bound
variable is a member of FV(G)
-abstraction whose bound
variable is a member of FV(G)  FV(H)
to an abstraction whose bound
variable is not a member of {u}
FV(H)
to an abstraction whose bound
variable is not a member of {u}  FV(G))
FV(G))
 FV(H).
FV(H).
Let (E' = ( u'.C') G)
and let v', D', H' be the converted forms of v,D,H.
u'.C') G)
and let v', D', H' be the converted forms of v,D,H.
Consider that by Lemma PT3.
= E'[p][u':=G] = (( v'.D') H)[u':=G]
v'.D') H)[u':=G]
= (( v'.D')[u':=G] H[u':=G])
v'.D')[u':=G] H[u':=G])
 -converted
to avoid variable-capture.
-converted
to avoid variable-capture.
= (( v'.D'[u':=G]) H[u':=G])
v'.D'[u':=G]) H[u':=G])
Which is a redex. So, we can work out
 (
( (E',()),p')
(E',()),p')
 (C'[u':=G]),p')
(C'[u':=G]),p')
 to
to
 (
( (E',p),())
(E',p),())
=  (E'[p:=D'[v':=H']],())
(E'[p:=D'[v':=H']],())
=
 (((
((( u'. C'[p':=D'[v':=H']])G)),())
u'. C'[p':=D'[v':=H']])G)),())
 is
is
= C'[p':=D'[v':=H']][u':=G]
= C'[u':=G][p':=D'[v':=H'][u':=G]]
 FV(G)
FV(G)  FV(H).
FV(H).
= C'[u':=G][p':=D'[u':=G][v':=H']]
 Thus we have shown that local-confluence holds for E', which
is
Thus we have shown that local-confluence holds for E', which
is  -congruent to E. Local confluence for
Eitself follows from
-congruent to E. Local confluence for
Eitself follows from  -conversion.
-conversion.