Computer Science 591i
Church-Rosser - Call-by-Value and Call-by-Name

Now let's try to tidy up the Church-Rosser Theorem for the

-calculus.

We don't need to worry about the case illustrated in the second figure, because it is converted into the case handled by Proposition LC2 by -conversion. The only case left to us to consider is that in which the inner redux occurs in the argument of the outer redux.

Recall the diagram of this case. If we perform the outer reduction before the inner one (the "call-by-name" case), we get a copy of the inner redux for every occurrence of the variable of the outer -bound variable in the body of the outer -abstraction.

If, on the other hand (the "call-by-value" case), we perform the inner reduction before the outer one, we get exactly one contractum of the inner redex, leaving us with a new version of the outer redex with that contractum in place of the inner redex.

Obviously, to achieve local confluence, we have to reduce those redexes (under discussion) which remain unreduced in each case. In the call-by-value case, the outer redex will be reduced, resulting in the substitution of the inner contractum for all occurrences of the variable of the lambda-abstraction of the outer redex in the body of that abstraction.

However, in the call-by-name case, the inner-redex has been copied zero or more times in the body of the lambda-abstraction of the outer redex. In order to bring this "call-by-name" reduction into line with the "call-by-value" case, we will have to reduce every one of the copies of the inner-redex. This means that we will need to show that the final substitution which occurs in the call-by-value case gives an identical result to multiple-constructive-updates along paths which are the effect of multiple applications of our function.

The practical result of this is that, since (in the call-by-value case) we have to separately reduce each copy of the inner-redux, we will use a distinct path to address each redux. We can characterise multiple -reductions by a sequence of paths, each of which addresses one redux-copy.

How are we to create this path-sequence? Well, let's observe that each copy of the inner-redux occurs in place of an ocurrence of the outer lambda-bound variable in the original outer-redux. Thus, if we can make a list of all paths to occurrences of a specified variable in an expression, we will be well placed to being able to use such a list (or finite sequence) as a way of specifying the -reductions required to bring the call-by-name form in line with the call-by-value one. This is achieved by the paths function, defined below.

However we have to show identity (up to -conversion) of substitution with multiple conversions along paths. This is achieved primarily by Lemma PT4 which shows that the substitution E[v:=F] can be accomplished by a series of updates of paths leading to v in E

However, before we can begin work upon this key lemma, we need to refresh our memory about various general functions defined on finite sequences which are familiar to users of functional languages, to whit map and reduce.

The reduce function (not to be confused with the term reduction as we have been using it) takes a binary operation as argument, and in essence uses that binary operation to combine elements of a finite sequence together. A second argument is supplied to provide a base for the combination. It helps us (or at least it helped me) to visualise what's going on if we write the binary operation infixed as o. Thus, if P is a sequence, then

₁

₂

In this, o associates to the right, to make this clear let's actually write:

₁

₂

It is essential to remember the right-associativity when we come to use reduce for real later.

An elementary example of the use of reduce is.

reduce(+,0,(3 4 5)) = 3 + 4 + 5 + 0 = 12

Definition of reduce

Let o: X >< Y->Y be a binary function, written infixed. Let s be a finite sequence of members of X .
Let y Y Then the reduce function is defined as follows:

RED1 reduce(o, y, ()) = y

RED2 reduce(o, y, x::s) = x o reduce(o, y, s)

Note

The reduce function as defined above is missing the first argument that the reduce function has in the 287 course.

We will also require the function map which transforms one finite sequence into another, making a systematic modification of every element. While this can be regarded as a special case of reduce, it's more convenient to define it separately.

Definition

Let f be a function. Let s be a finite sequence.

MAP1 map(f, ()) = ()

MAP2 map(f, x::s) = f(x) :: map(f,s)

We will also need the concept of concatenating two finite sequences. Let's define this thus

Definition

The concatenation function, written infix as "<>", is defined by:

CC1 () <> s = s

CC2 (x::s) <> t = x::(s<>t)

We also need the concept of the extension of a path by one step. This is simply related to the sequence-constructor operation "::".

Definition

EXT1 ext(s)(p)=s::p

Definition

Let E be a term of the

-calculus. Let v be a variable. Then the paths leading to v in E, written paths(E,v) are the sequence of paths defined as follows.

PL1 paths(v,v) = ((v))

PL2 paths(u,v) = (())

PL3 paths(c,v) = (())

PL4 paths((F G),v) = map(ext(0),paths(F,v)) <> map(ext(1),paths(G,v))

PL5 paths(( v. H),v) = ()

PL6 paths(( u. H),v) = map(ext(1), paths(H,v))

Now the above definition of paths makes use of the concatenation operator "<>", as well as the map function. Our general strategy will be to use the reduce function to combine the effects of multiple -reductions. Thus inevitably reduce is going to interact with "<>" and with map. Let's prove a couple of lemmas that address that interaction.

The following lemma is fairly obvious if we think about reduce in the right way. Suppose, for example, we have two path-sequences P and P'. Then

₁

₂

₁

₂

_n'

We can, by emphasising the bracketing, easily see that the RHS can be seen as

₁

₂

(

₁

₂

_n'

)

so, it's not surprising that we can treat such a beast as a nested application of reduce.

Lemma Red1

Let l₁ l₂ be two finite sequences. Let o be a binary function, written as an infix. Then

₁

₂

₁

Proof

By induction on length(l₁)

Base Case

If length(l₁) = 0 then l₁ = ().

On the one hand, from the definition of "<>".

reduce(o, b, l₁ <> l₂) = reduce(o, b, l₂)

On the other hand, since l₁=(), by the definition of reduce we have:

₂

₁

₂

= reduce(o,b,l₂)

Hence the result holds in the base case.

Inductive Step.

Suppose for all sequences l for which length(l) = n that

₁

₂

₁

we have to show that the result holds for a sequence s::l where length(l) = n. Applying first the definition of "<>" and then the definition of reduce we obtain

₂

= s o reduce(o,reduce(o,b,l₂),l)

by the inductive hypothesis. On the other hand, using the definition of reduce we obtain

₂

Hence the result holds for any sequence s::l of length n+1. Hence the result holds for all finite sequences.

Note

It's worth noting that the proof of the above lemma is independent of any algebraic properties (such as associativity) of the o operation.

Next we come to the interaction of reduce and the use of map in the definition of paths. In this case, we prove lemmas specific to the actual use of map in the definition of paths. These lemmas are motivated by the requirements of Lemma PT4, which shows how substitution can be performed using path-updates - so those seeking motivation of the immediate lemmas should perhaps look first at PT4.

Lemma Red2

Let F, G, H be terms of the lambda-calculus. Let P be a sequence of paths. Let us define the infix operation o to be, for any path p and any term E

Then

Proof

By induction on length(P)

Base Case
reduce(o,(G H), map(ext(1),())) = (G H)
On the other hand
(G reduce(o,H,()) = (G H)

Inductive Step

Suppose that for all path-sequences of length n that

Consider a path-sequence p::P of length n+1.

reduce(o,(G H), map(ext(1),p::P))

=reduce(o,(G H), (1::p) :: map(ext(1),P))

by the definition of map, ext

= (1::p) o reduce(o,(G H), (1::p) :: map(ext(1),P))

by the definition of reduce

(1::p) o (G reduce(o,H,P))

by the inductive hypothesis. Now, using the definition of o and of path-update, we obtain

= (G reduce(o,H,P))[(1::p) := F]

= (G reduce(o,H,P)[p := F])

= (G p o reduce(o,H,P))

= (G reduce(o,H,p::P))

Hence the result holds for any path-sequence of length n+1. Hence, by the principle of induction, the result holds for all finite sequences of paths.

Lemma Red3

Let F, G, H be terms of the lambda-calculus. Let P be a sequence of paths. Let us define the infix operation o to be, for any path p and any term E

Then

Proof

Similar to Lemma Red2

Lemma Red4

Let F, G be terms of the lambda-calculus. Let P be a sequence of paths. Let us define the infix operation o to be, for any path p and any term E

Then

Proof

Similar to Lemma Red2

Building a connection between path-updates and substitution.

This case of the Church Rosser Theorem requires us to show that a substitution (of the reduced argument in the body of the lambda-abstraction of the outer redux) is equivalent to multiple reductions along a variety of paths. Now it is intuitively obvious that a substitution can be accomplished by multiple tree-updates along paths. The following lemma formalises this.

Lemma PT4

Let E,F be a expressions of the lambda-calculus, and let v be a variable. Suppose no variable free in F is bound in E. Let us write the infixed o operation to mean

then

Proof

By induction of the height of E.

Suppose E = v. Now from PL1, there is one path to v, of no steps.
and, from the definition of reduce
Thus
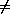Suppose E = u, a variable u v
Suppose E = c, a constant. This case is similar to the previous one.

Inductive Step

Suppose for all E for which height(E) n we have that

We have to show that the result holds for E for which height(E)=n+1

Suppose E = (G H), an application. Then, by PL4
Hence using Lemma Red1 we obtain
Now consider the inner reduce term. We apply Lemma Red2 to this.
by the inductive hypothesis. Substituting in the full expression
which by a similar use of Lemma Red2 is seen to be
So the lemma holds in this case (Phew! - and there's more to come).
Suppose E = v.H
On the other hand
Concluding this case.
Suppose E = u.H , u 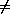v. Then
Now, because no variable free in F is bound in E
by Red4. And, from the inductive hypothesis we have

Unfortunately we've defined the

-function to have its arguments the wrong way round for the smoothest statement of the next result. But here goes:

Computer Science 591i Church-Rosser - Call-by-Value and Call-by-Name

Definition of reduce

Note

Definition

Definition

Definition

Definition

Lemma Red1

Proof

Base Case

Inductive Step.

Note

Lemma Red2

Proof

Base Case reduce(o,(G H), map(ext(1),())) = (G H) On the other hand (G reduce(o,H,()) = (G H)

Inductive Step

Lemma Red3

Proof

Lemma Red4

Proof

Building a connection between path-updates and substitution.

Lemma PT4

Proof

Inductive Step

Computer Science 591i
Church-Rosser - Call-by-Value and Call-by-Name

Base Case
reduce(o,(G H), map(ext(1),())) = (G H)
On the other hand
(G reduce(o,H,()) = (G H)