Computer Science 591i
A Tree-Surgeon's Approach to the Church-Rosser Theorems
Note
Subsequently I have had cause to repent of my laxity in the definition
of addressing exhibited in PH2,PH3 below.
Now let us turn our attention to one of the most important classes of
theorem of the  -calculus - the Church-Rosser theorems.
We have seen that we can think of computation as being characterised in the
-calculus - the Church-Rosser theorems.
We have seen that we can think of computation as being characterised in the
 -calculus by the application of
-calculus by the application of  -reduction rules, which nessarily, by S7, require certain
-reduction rules, which nessarily, by S7, require certain  -conversions. However, in general, a term of the
-conversions. However, in general, a term of the  -calculus will contain several
-calculus will contain several  -redexes,
and on the face of it there is no particular reason to choose to reduce one
rather than another.
-redexes,
and on the face of it there is no particular reason to choose to reduce one
rather than another.
We could, of course, make an arbitrary choice, which, if we are
implementing our reduction computationally, will amount to doing a
reduction that some kind of reduction-algorithm selects. A better approach
is to study the consequences of making choices. The result of this is that
we can prove theorems, the Church Rosser theorems, which show that
- No individual choice of redex is irrevocably wrong.
- However, applying the wrong choice strategy can lead to
a computation that doesn't terminate, even though there is a "right"
answer which we could have found using the right strategy.
Let's consider how we might choose a redex. For example, let
G = (( x . E) F)
x . E) F)
where there are redexes in F. To be more specific, we might have:
(( x . x+1) ((
x . x+1) (( y . y+2) 4))
y . y+2) 4))
We could choose to reduce F before the top-level redux
in G, or after. Now most programming languages in effect in most cases
choose to reduce F before doing the top-level redux. The
"call-by-value" rule of Scheme, say, says "evaluate the arguments, and then
apply the function to the evaluated arguments". However this can't be the
universal rule, for consider any recursive definition such as
the SML:
fun fact(n) = if n=0 then 1 else n*fact(n-1)
or, in Scheme:
(define fact (lambda(n) (if (= n 0) 1 (* n (fact (- n 1))))))
Now if we are evaluating the if expression, we must not
evaluate all its arguments, or the recursion will not terminate - think,
for example if we replaced if in the above definition of
the factorial function by my_if defined by
(define my_if (lambda (a b c) (if a b c)))
The recursion surely wouldn't terminate.
Scheme gets round this problem by making an if-expression be a
special form, which is evaluated according to its own rules, which
in effect reduce the first argument of if and see what the result
is before deciding whether to reduce the second or third argument of the
if-expression.
Now mathematicians don't like special cases. You can see why if you
reflect on our proofs relating to substitution. Almost every proof had
seven cases, arising from clauses S1-S7 of the definition of substitution.
And some of the cases had sub-cases. For example in the free-variable
lemma, Sub.1, some of the cases had sub-cases, arising in effect from the
sub-cases of the definition of set-union,
x  S
S  T if
[case 1] x
T if
[case 1] x  S OR
[case 2] x
S OR
[case 2] x  T.
T.
In general, if we have a definition of a concept C1 that has
n1 cases and a definition of a concept C2 that has
n2 cases then a theorem involving both concepts might
have as many as n1n2 cases. Clearly this can
get out of hand.
So, wouldn't it be nice if we could define a concept of how to evaluate
an expression that didn't require any special rules for particular kinds of
expression (except of course  -abstractions and we can even get rid of these).
-abstractions and we can even get rid of these).
The Figures
Case 1
Case 2
Case 3
Case 4
We can begin see how to attack this problem if we consider the diagram
(Church-Rosser Theorem Case 1). The convention used in this and subsequent
diagrams is that a bold triangle stands for a term of the
 -calculus. If one triangle Fis
contained in another triangle E then this means that F is
a sub-term of E.
Triangles with a small triangle at the top, containing
a letter, stand for
-calculus. If one triangle Fis
contained in another triangle E then this means that F is
a sub-term of E.
Triangles with a small triangle at the top, containing
a letter, stand for  -abstractions, while occurrences of
a letter along the base of the triangle stand for occurrences of a variable
in an term (usually the bound variable of a lambda-abstraction).
The light lines are intended to indicate how a sub-term relates to its
super-term.
-abstractions, while occurrences of
a letter along the base of the triangle stand for occurrences of a variable
in an term (usually the bound variable of a lambda-abstraction).
The light lines are intended to indicate how a sub-term relates to its
super-term.
The Case 1 diagram illustrates the simplest circumstances for the
Church-Rosser theorem. The term E has two sub-terms, F
and G each of which has the form of an application of a  -abstraction applied to an argument. F is indicated
by an @-node with a
-abstraction applied to an argument. F is indicated
by an @-node with a  -abstraction immediately below it
to the left, while its argument is indicated by the shaded triangle to the
right. G is indicated similarly. Since both F and
G are redexes, we can choose to reduce either. If we beta-reduce
F, as indicated by the dotted arrow going to the left we obtain a
new term E1. Likewise if we beta-reduce
G, as indicated by the dotted arrow going to the right
we obtain a
new term E2.
-abstraction immediately below it
to the left, while its argument is indicated by the shaded triangle to the
right. G is indicated similarly. Since both F and
G are redexes, we can choose to reduce either. If we beta-reduce
F, as indicated by the dotted arrow going to the left we obtain a
new term E1. Likewise if we beta-reduce
G, as indicated by the dotted arrow going to the right
we obtain a
new term E2.
However, whether we choose to reduce F or G it is
clear enough, at least at this diagramatic level, that we can reduce both
E1 and E2
to a common form E12.
Case 1 is of course the simplest case, in which the two reduxes are
disjoint - they have nothing in common. Other cases, as you will see by
perusing this document, are somewhat more complex.
Confluence, local and global
Moreover, the diagrams show only what happens if we take just one step
of reduction. The full Church-Rosser theorem requires that no matter how
many steps of reduction we have taken, we can always get back to a common
term. We can, however, by relatively easy steps, build up the full theorem.
Definition
A relation  is said to be
(globally) confluent if, given
E,F,G which are terms of the
is said to be
(globally) confluent if, given
E,F,G which are terms of the  -calculus,
-calculus,
E  * F
* F
E  * G
* G
there exists H, a term of the  -calculus,
for which
-calculus,
for which
F  * H
G
* H
G  * H
* H
Proving global confluence is a bit much to bite off in one proof. Actually,
in terms of the nitty-gritty of our theory it is enough to prove
local confluence.
Definition
A relation  is said to be locally
confluent if, given
E,F,G which are terms of the
is said to be locally
confluent if, given
E,F,G which are terms of the  -calculus,
-calculus,
E  F
F
E  G
G
there exists H, a term of the  -calculus,
for which
-calculus,
for which
F  * H
G
* H
G  * H
* H
Notice that, with local confluence, we may have to take several steps
to reach the common term H. It's a bit like a railway system - get
on the wrong train and you can still reach your destination, but it may
take several steps to get there.
Planning our proof
Now a set of diagrams like the Case 1-4 diagrams do not constitute a
proof of any part of the Church-Rosser theorem. But they do provide a good
basis on which to plan a proof.
So, let's adopt a strategy of specifying algorithmically how we can
implement this local confluence property. Informally we may say "if we
transform E to E1 by reduction of the redex
F to F1, and we
transform E to E2 by reduction of
the redex G to G2
then we can transform E1 to E12
by reduction of the redex G to G2, and
we can also transform E2 to E12
by reduction of the redex F to F1".
However
this leaves us with the problem of "what do we mean by 'the redex
G' when we are speaking of E1. For
E1 is a different term from E. It's not enough
to say "the sub-term that's congruent to G in the original term",
because G might occur more than once. The hacker's solution to
this kind of problem would be to specify how to find a sub-term in
a tree by following a path in that tree. We can think of a path
as a sequence of the digits "0" and "1", with the idea that "0" means "go
left" and "1" means "go right". Thus a path acts as a kind of
address for sub-terms of the tree (actually, if you think about
it, an address in hardware also corresponds to a path through a tree).
More precisely we may say:
Definition
Let p be a non-empty path. Then the head of p, written
hd(p), is the first element of p, and the tail of
p, written tl(p) is the sequence consisting of all
elements of p bar the first.
The
attentive reader who has encountered LISP may think of hd and
tl as CAR and CDR respectively; we use the POP-2
names as being a little more mnemonic.
Following the POP-2 convention, we will also write s::p for
the path whose head is s and whose tail is p.
We are now ready to define our sub-tree addressing operation. We
will write this as E[p] - it can be thought of as a kind of
generalisation of array-access.
Definition
Let E be a term of the  -calculus. Let
p be a path. Then the subterm of E addressed by p is
defined to be
-calculus. Let
p be a path. Then the subterm of E addressed by p is
defined to be
PH1 if p = () then E[p] = E
PH2 if E = u, a variable, then E[p] = u
PH3 if E = c, a constant, then E[p] = c
PH4.1 if E = (F G), an application, and hd(p) = 0,
then E[p] = F[tl(p)]
PH4.2 if E = (F G), an application, and hd(p) = 1,
then E[p] = G[tl(p)]
PH5.1 if E =  x.G, an abstraction, and
hd(p) = 0, then E[p] = x
x.G, an abstraction, and
hd(p) = 0, then E[p] = x
PH5.2 if E =  x.G, an abstraction, and
hd(p) = 1, then E[p] = G[tl(p)]
x.G, an abstraction, and
hd(p) = 1, then E[p] = G[tl(p)]
As well as the addressing operation, we need to define our
constructive update.
Definition
UP1 if p = () then E[p:=F] = F
UP2 if E = u, a variable, then E[p:=F] = E
UP3 if E = c, a constant, then E[p:=F] = E
UP4.1 if E = (F G), an application, and hd(p) = 0,
then E[p:=H] = (F[tl(p):=H] ,G)
UP4.2 if E = (F G), an application, and hd(p) = 1,
then E[p:=H] = (F, G[tl(p):=H])
UP5.1 if E =  x.G, an abstraction, and
hd(p) = 0, then E[p:=F] = E
x.G, an abstraction, and
hd(p) = 0, then E[p:=F] = E
UP5.2 if E =  x.G, an abstraction, and
hd(p) = 1, then E[p:=F] =
x.G, an abstraction, and
hd(p) = 1, then E[p:=F] =
 x.G[p:=F]
x.G[p:=F]
We can now define  as a function. However, we need to
be sure to distinguish between the substitution E[u:=F] where
u is a variable of the
as a function. However, we need to
be sure to distinguish between the substitution E[u:=F] where
u is a variable of the  -calculus,
and the path-update E[p:=F] in which p is a path.
So, we'll use p,q,r for paths, and restrict
ourselves to u,v,w,x,y,z for variables of the
-calculus,
and the path-update E[p:=F] in which p is a path.
So, we'll use p,q,r for paths, and restrict
ourselves to u,v,w,x,y,z for variables of the  -calculus.
-calculus.
Definition
if E[p] = (( u. F) G) then
u. F) G) then
 (p,E) = E[p:=F[u:=G]]
(p,E) = E[p:=F[u:=G]]
Otherwise  (p,E) = E
(p,E) = E
It may be objected that in cases PH2
and PH3 we have not required that the path be empty, despite the fact that
it is meaningless to have a non-empty path here. The convention adopted has
the advantage that we don't have to worry about defining a mathematical
equivalent of throwing an exception. We'll try to ensure that the paths we
actually specify will not "run out of tree".
With this idea of a path, we can see how to write a program for
local confluence.
We are just about ready to state a proposition which covers one case of
local confluence. It is in fact a special case of that shown in the Case-1
diagram, in which the paths to the sub-terms F and G
diverge. We'll prove a number of these propositions, and then
"glue" them together to show local confluence in the case when two paths
have a common initial section.
Proposition LC.1
If E is a term of the  -calculus and p
and q are paths for which hd(p)
-calculus and p
and q are paths for which hd(p) 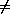 hd(q) then
hd(q) then
Discussion
This is certainly the easiest case to handle, because we don't have to
consider the mechanism of  -reduction at all. Essentially,
all we have to show is that if you have a tree and replace distinct parts
of it, it doesn't matter in which order you do the replacements.
Let us abuse (or at least overload) our
notation somewhat by writing E[p:=F] for that
expression which is obtained from E by replacing the subterm addressed
by p by F. This allows us to specify the replacement of
one branch of a tree by another.
-reduction at all. Essentially,
all we have to show is that if you have a tree and replace distinct parts
of it, it doesn't matter in which order you do the replacements.
Let us abuse (or at least overload) our
notation somewhat by writing E[p:=F] for that
expression which is obtained from E by replacing the subterm addressed
by p by F. This allows us to specify the replacement of
one branch of a tree by another.
We defer the proof of LC.1
We saw in our preliminary discussion on the Church-Rosser Theorem that the
subterm relationship
between two candidate redexes G and H, say,
of a given term E crucially determined the various cases of the
Theorem. In turn G and H can be classified by the
paths that address them. Two paths p,q can be classified as
-
p = q
- p is a sub-path of q
- q is a sub-path of p
- p and q diverge.
We can define the following function PC, which classifies the
relationship between two paths.
Definition
PC1 PC([],[]) = '='
PC2 PC([],s::p) = '<'
PC3 PC(s::p,[]) = '>'
PC4 PC(s::p,t::q) = 'I' if s 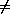 t
t
PC5 PC(s::p,t::q) = PC(p,q) if s = t
Proofs involving paths will be by mathematical induction, for which we'll
need a numeric measure of various aspects of paths. The following function
computes the length of the common part, CP, of two paths.
Definition
CP1 CP([],[]) = 0
CP2 CP([],s::p) = 0
CP3 CP(s::p,[]) = 0
CP4 CP(s::p,t::q) = 0 if s 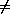 t
t
CP5 CP(s::p,t::q) = 1+CP(p,q) if s = t
Lemma PT1
If p, q are binary paths for which PC(p,q) = 'I', and
E,F,G
are terms of the  -calculus, then
E[p:=F][q:=G] = E[q:=G][p:=F]
-calculus, then
E[p:=F][q:=G] = E[q:=G][p:=F]
Proof
By induction on CP(p,q)
Base Case
Suppose CP(p,q) = 0. If PC(p,q) = 'I' then we must have
p = s::p', q = t::q', s 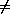 t
t
We can assume W.L.O.G. that s=0,t=1.
- Case 1-2: E is a constant or variable. In this case
E[p:=F][q:=G] = E[q:=G] = E
E[q:=G][p:=F] = E[p:=F] = E
- Case 3: E = (C D), an application.
E[p:=F][q:=G] = (C[p':=F] D)[q:=G] = (C[p':=F] D[q':=G])
E[q:=G][p:=F] = (C D[q':=G])[p:=F] = (C[p':=F] D[q':=G])
- Case 4: E =
 x . H, an abstraction.
x . H, an abstraction.
E[p:=F][q:=G] = ( x . H)[p:=F][q:=G]
= (
x . H)[p:=F][q:=G]
= ( x . H)[q:=G]
x . H)[q:=G]
= ( x . H[q':=G])
x . H[q':=G])
E[q:=G][p:=F] = ( x . H)[q:=G][p:=F]
=(
x . H)[q:=G][p:=F]
=( x . H[q':=G])[p:=F]
x . H[q':=G])[p:=F]
=( x . H[q':=G])
x . H[q':=G])
Inductive Step
Suppose for some natural number n that
CP(p,q)  n implies that
n implies that
E[p:=F][q:=G] = E[q:=G][p:=F]
Consider paths p,q for which CP(p,q) = n+1
We must therefore be confronting case CP5 in which
p = s::p', q = s::q'. Moreover CP(p',q') = n
Lemma PT2
If p, q are binary paths for which PC(p,q) = 'I', and E,F
are terms of the  -calculus, then
E[p:=F][q] = E[q]
-calculus, then
E[p:=F][q] = E[q]
Proof
By induction on CP(p,q)
Base Case
Suppose CP(p,q) = 0. If PC(p,q) = 'I' then we must have
p = s::p', q = t::q', s 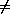 t
t
Inductive Step
Suppose for some natural number n that
CP(p,q)  n implies that
Consider paths p,q for which CP(p,q) = n+1
We must therefore be confronting case CP5 in which
p = s::p', q = s::q'. Moreover CP(p',q') = n
n implies that
Consider paths p,q for which CP(p,q) = n+1
We must therefore be confronting case CP5 in which
p = s::p', q = s::q'. Moreover CP(p',q') = n
- Case 1-2: E is a constant or variable. In this case
E[p:=F][q] = E[q] = E
- Case 3: E = (C D), an application.
We have 2 sub-cases,
s=0 and s=1
- Case 4: E =
 x . H, an application.
We have 2 sub-cases,
s=0 and s=1
x . H, an application.
We have 2 sub-cases,
s=0 and s=1
- Sub-case 4.1, s=0
E[p:=F][q] = ( x . H)[p:=F][q]
= (
x . H)[p:=F][q]
= ( x . H)[q] = x = E[q]
x . H)[q] = x = E[q]
- Sub-case 4.2, s=1
by the inductive hypothesis.
On the other hand
So the result holds for this sub-case.
Proof of Proposition LC.1
We have to show that
Let us recall the definition of the  -function.
-function.
if E[p] = (( u. F) G) then
u. F) G) then
 (p,E) = E[p:=F[u:=G]]
(p,E) = E[p:=F[u:=G]]
Otherwise  (p,E) = E
(p,E) = E
The interesting case is:
Case 1
E[p] = (( u. D) G) and
u. D) G) and
E[q] = (( v. F) H)
v. F) H)
Here
since, by Lemma PT2, E[p:=D[u:=G]][q] = E[q]
Likewise
But, by Lemma PT1 [1] and [2] are equal.
Case 2
E[p] = (( u. D) G) and
u. D) G) and
E[q] is not a  -redux
-redux
Here
since, by Lemma PT2, E[p:=D[u:=G]][q] = E[q]
On the other hand
 (
( (E,q),p) =
(E,q),p) =
 (E,p) = E[p:=D[u:=G]] ______[2]
(E,p) = E[p:=D[u:=G]] ______[2]
But, since [1] and [2] are equal, the result holds in this case.
Case 3
E[p] is not a  -redux
-redux
E[q] = (( v. F) H)
v. F) H)
This case is the dual of case 2.
Case 4
E[p] is not a  -redux
-redux
E[q] is not a  -redux
-redux
In this case
 (
( (E,p),q) =
(E,p),q) =
 (E,q) = E =
(E,q) = E =
 (
( (E,q),p)
(E,q),p)
This concludes the proof of Proposition LC.1
As we have already remarked, Proposition LC1 addresses the simplest case
of proving local-confluence, that in which the redexes are independent, as
characterised by having PC(p,q) = 'I'. The other cases are harder (apart
from the trivial p=q case).
Proposition LC1 did not depend on any properties of the substitution
operation, only assuming it is a function. [Note - we'd better make
sure it is by being more precise about our specification of
w in S6].
The
case in which PC(p,q) = '>' is symmetric with that in which PC(p,q) =
'<', so we need only consider one of them.
Essentially, if PC(p,q) = '<', then the redex addressed by
p(if any) contains that addressed by q(if any).
However we need to worry about where E[q] is to be found in
E[p] = (( u. D) G) - it could be in either
D or in G.
u. D) G) - it could be in either
D or in G.
NOTES
Shonfinkel Combinators
It is possible to translate from the
 -calculus to Shonfinkel combinators, S,K,I
More on these later.
-calculus to Shonfinkel combinators, S,K,I
More on these later.
 -calculus - the Church-Rosser theorems.
We have seen that we can think of computation as being characterised in the
-calculus - the Church-Rosser theorems.
We have seen that we can think of computation as being characterised in the
 -calculus by the application of
-calculus by the application of  -reduction rules, which nessarily, by S7, require certain
-reduction rules, which nessarily, by S7, require certain  -conversions. However, in general, a term of the
-conversions. However, in general, a term of the  -calculus will contain several
-calculus will contain several  -redexes,
and on the face of it there is no particular reason to choose to reduce one
rather than another.
-redexes,
and on the face of it there is no particular reason to choose to reduce one
rather than another.
 S
S  T if
[case 1] x
T if
[case 1] x  is said to be
(globally) confluent if, given
E,F,G which are terms of the
is said to be
(globally) confluent if, given
E,F,G which are terms of the 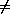 hd(q) then
hd(q) then
 n implies that
n implies that